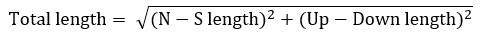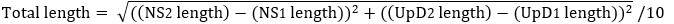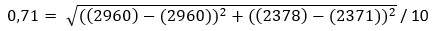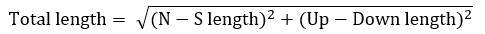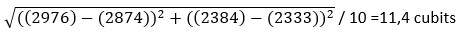The Horizontal Passageway
Section 5.7.1
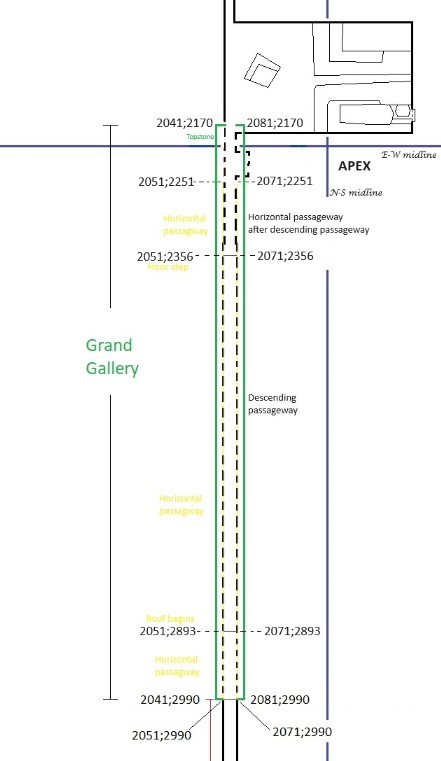
The horizontal passage is strange in many ways. It starts at the floor of the Grand Gallery, in a special section of the pyramid, I call the section the "Heart of The Pyramid". This section is connected to all other passageways and chambers in the pyramid. Upwards through the Grand Gallery to the "Kings Chamber", downwards to the exit through the ascending passageway or through the Well Shaft to the Grotto, the descending passageway and the Subterranean chamber and to the south through the horizontal passageway leading to the "Queens Chamber".
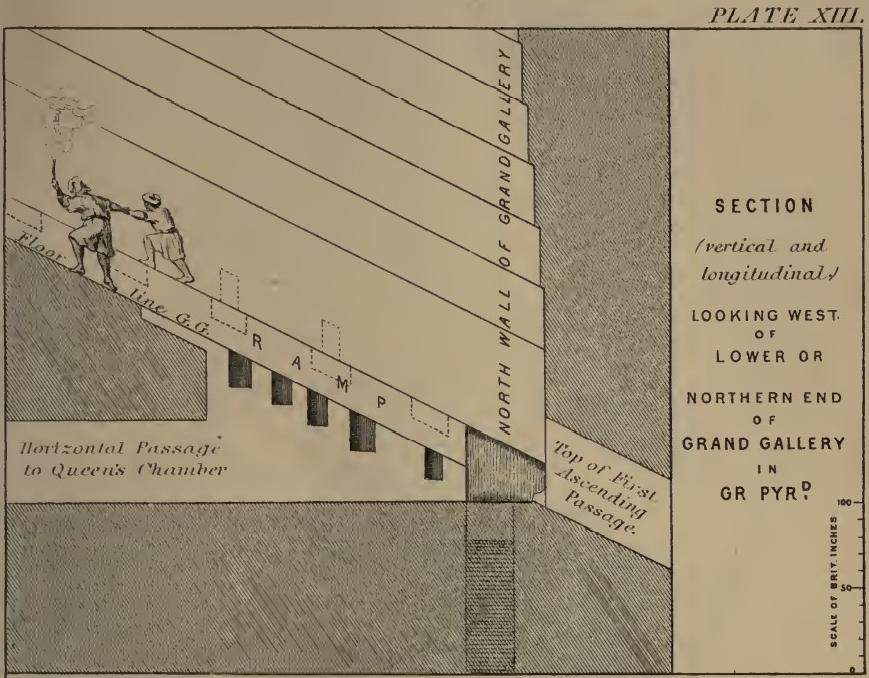
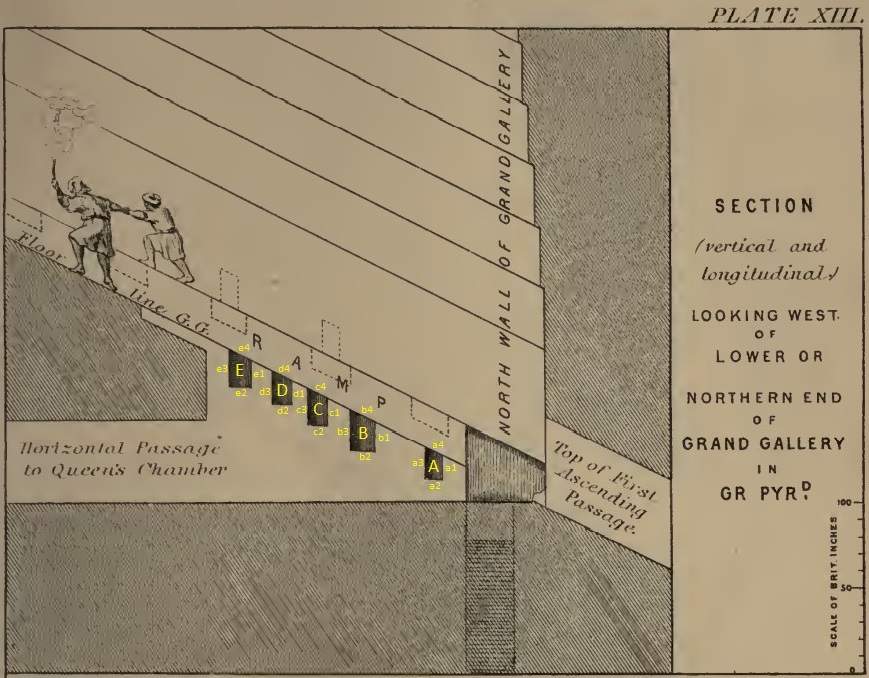
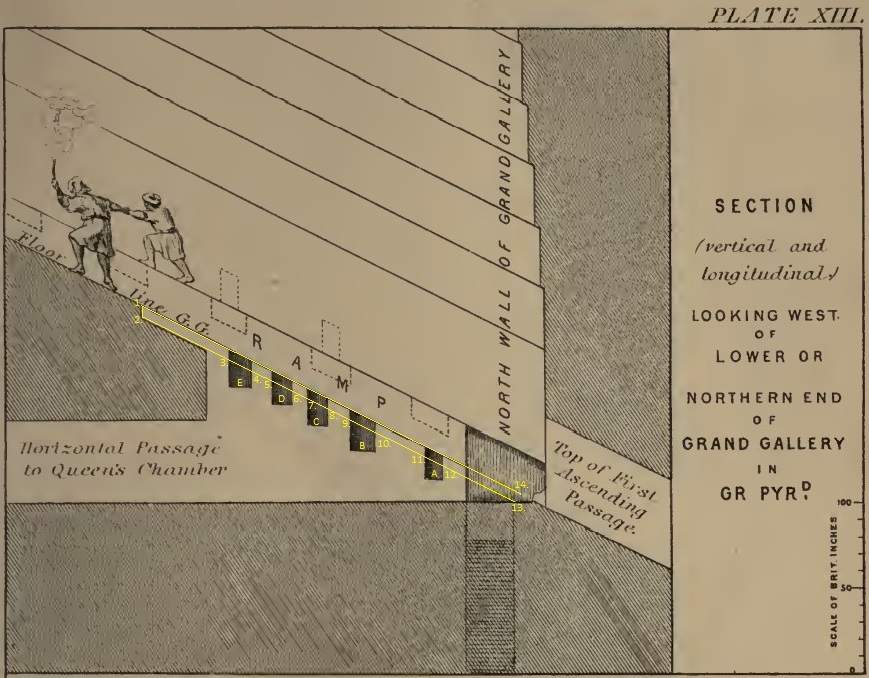
Let us see how the special section or cross section looks like, I have chosen a wonderful drawing by Piazzi Smyth published in his book "The Great Pyramid Its Secrets and Mysteries Revealed" published in 1880:S21. "The Great Pyramid Its Secrets and Mysteries Revealed" by C. Piazzi Smyth , Plate XIII between pages 226 and 227 after the chapter "Corrigenda".
The drawing is amazing because it has a "spirit", and the measures seems to be in accordance to my overall Master drawing. Furthermore, it is without any damages of the holes in the wall (the dark fields).
Edgar published a picture of the same section from North to South:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 , (page 291)
Behind and in front of Edgar you can see the holes in the walls are damaged.
Section 5.7.2
The amount of data for this section is very limited, so I must analyze the above drawing from Piazzi Smyth.
However, from section 5.5.6 we know certain coordinates which are important for the verification of the data which appear from the calculations underneath.
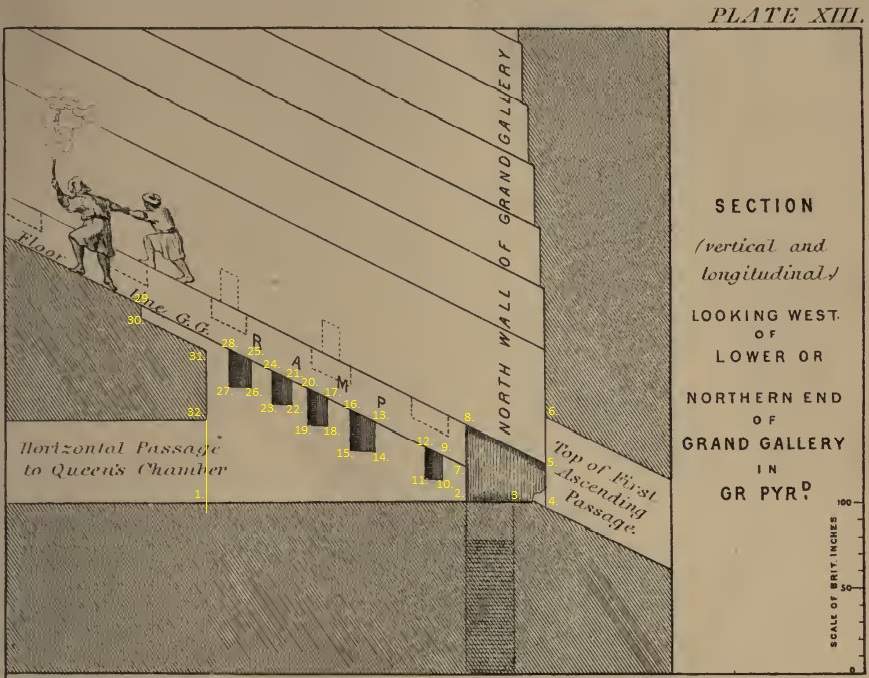
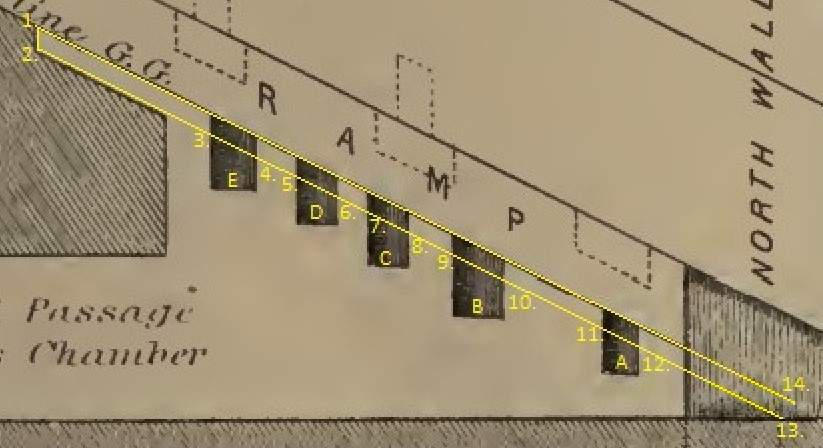
I have added numbers on the drawing of Piazzi at relevant corners:
S21. "The Great Pyramid Its Secrets and Mysteries Revealed" by C. Piazzi Smyth , Plate XIII between pages 226 and 227 after the chapter "Corrigenda". (Revised version).
The added yellow line between 1. and 32. indicates the vertical position of where the roof of the horizontal passageway begins.
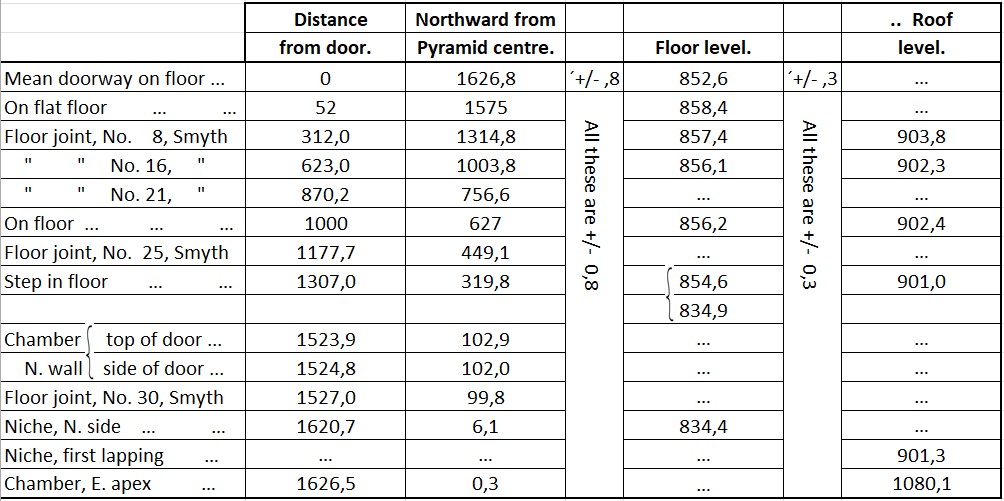
The height from 1. to 32. is measured by Flinders Petrie:
Source: (S5 orig-[S40]-P66-L5), table.
My comments:
Roof level 903,8" = 43,83 cubits RM and floor level 857,4" = 41,58 cubits RM
The height of the entrance of the horizontal passageway is 43,83 cubits RM - 41,58 cubits RM = 2,25 cubits RM. (In the Master drawing it is equal to 23 pixels.)
The level of the floor is 2800 pixels - 416 pixels = 2384 pixels, which is the Up-Down coordinate for the floor at this point.
The level of the roof is 2800 pixels - 438 pixels = 2362 pixels, which is the Up-Down coordinate for the roof at this point. The calculated value in the table underneath at the point 32 is 2361 pixels.
S.20. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, Vol. II, page 57 (part of the table).
My comments:
199,4" = 9,67 cubits RM
9,67 cubits RM x 1,0035 = 9,70 cubits RM ( = 97 pixels )
The northern N-S coordinate is 2990.
The N-S coordinate of the roof at the horizontal passageway is 2990 - 97 = 2893.
There are small (acceptable) deviations in the table, which are caused by inaccurate readings or maybe very small drawing errors.
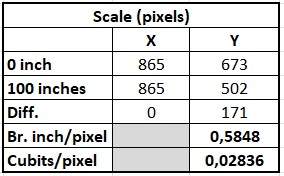
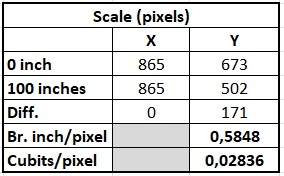
Fortunately, did Piazzi Smyth add a scale 0 - 100 British inches. This gives me an oppotunity to find the factor between the inches and the pixels in the drawing tool:100 inches / 171 pixels = 0,5848
The factor between the British inch and the cubit is 1/20,62
0,5848 / 20,62 = 0,02836
Section 5.7.3
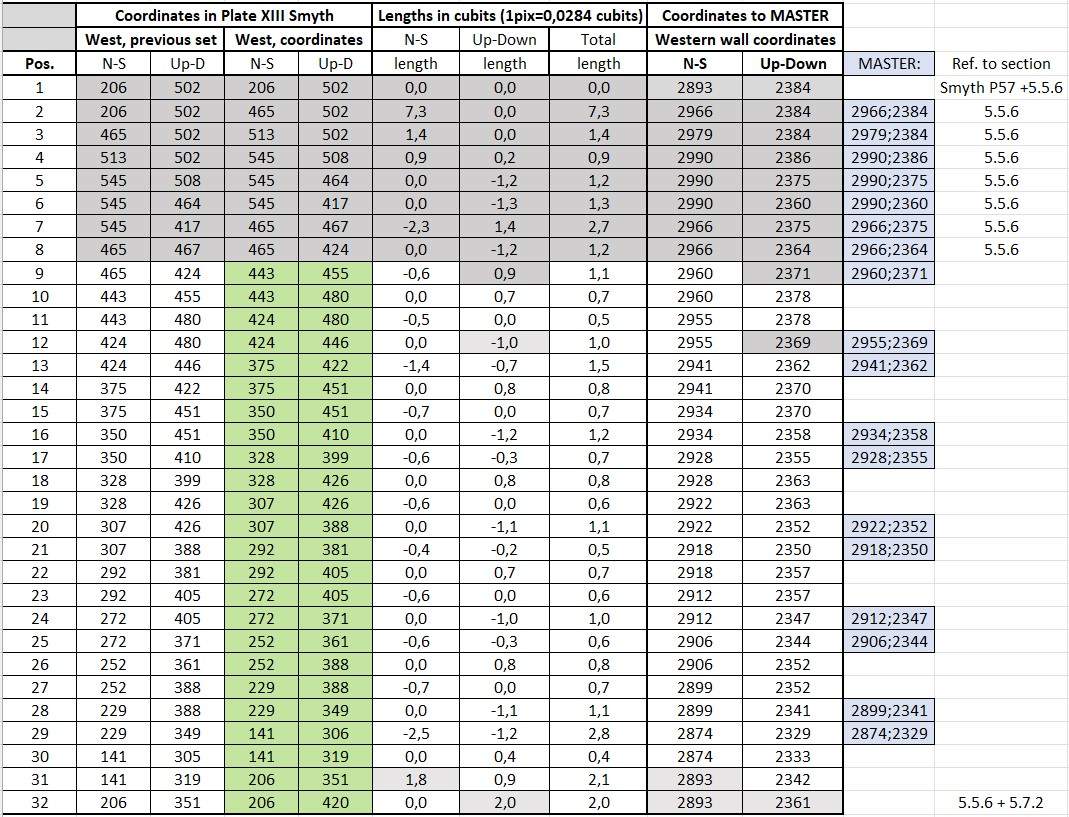
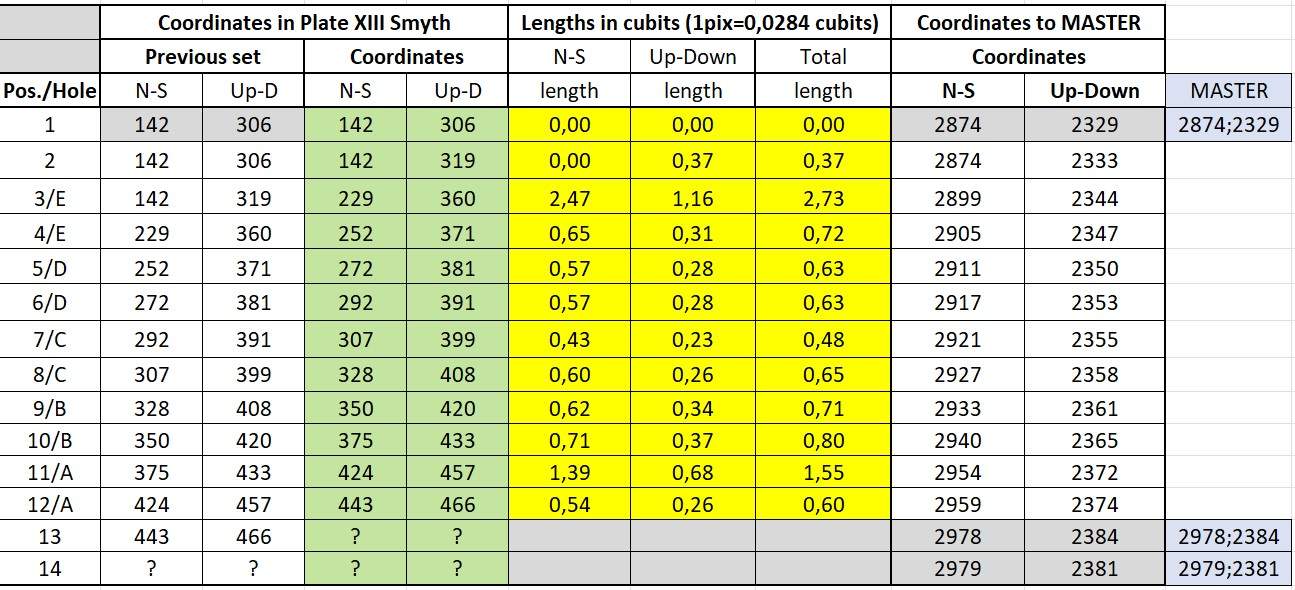
In this overview I have chosen to insert fixed reference points marked grey from the Master drawing. The references are mentioned on the right side of the table.
There are few minor deviations, I have marked these grey as well. The deviations are probably caused by a bad reprint, drawing error or a reading error.
The holes in the opposite wall have the same coordinates.
Calculation method:
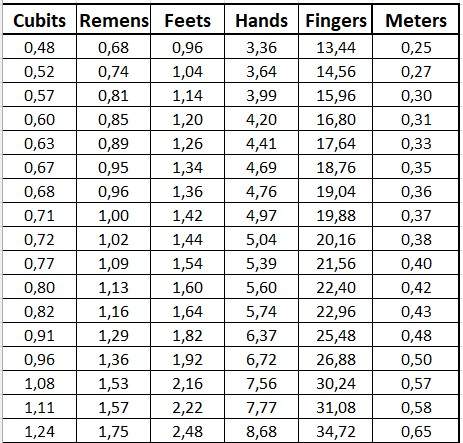
The dimensions of the holes in cubits are:
Source: S21, The Great Pyramid Its Secrets and Mysteries Revealed, Plate XIII between pages 226 and 227 after the chapter "Corrigenda". (Revised version).
Calculation method:
Example (from pos. 10 to pos. 9) :
For nerds I have issued an overview of the above mentioned hole dimensions with conversions. Maybe somebody can find a structure:
Section 5.7.4
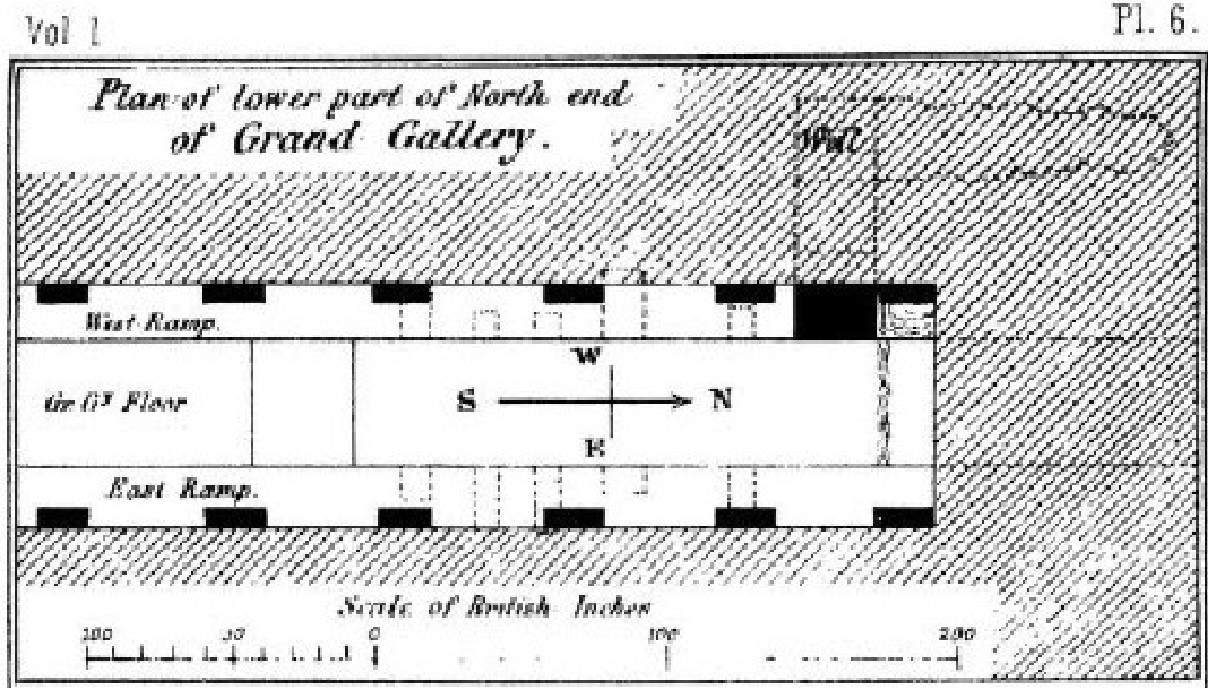
The depths of the holes into the walls are a bit trickier as I have no measuring data. but I have a poor drawing by Piazzi Smyth in a low quality as it is a reprint. From this drawing it is possible to extract data and calculate the depths in cubits more or less accurate. Still, it gives us an idea of the overall picture.
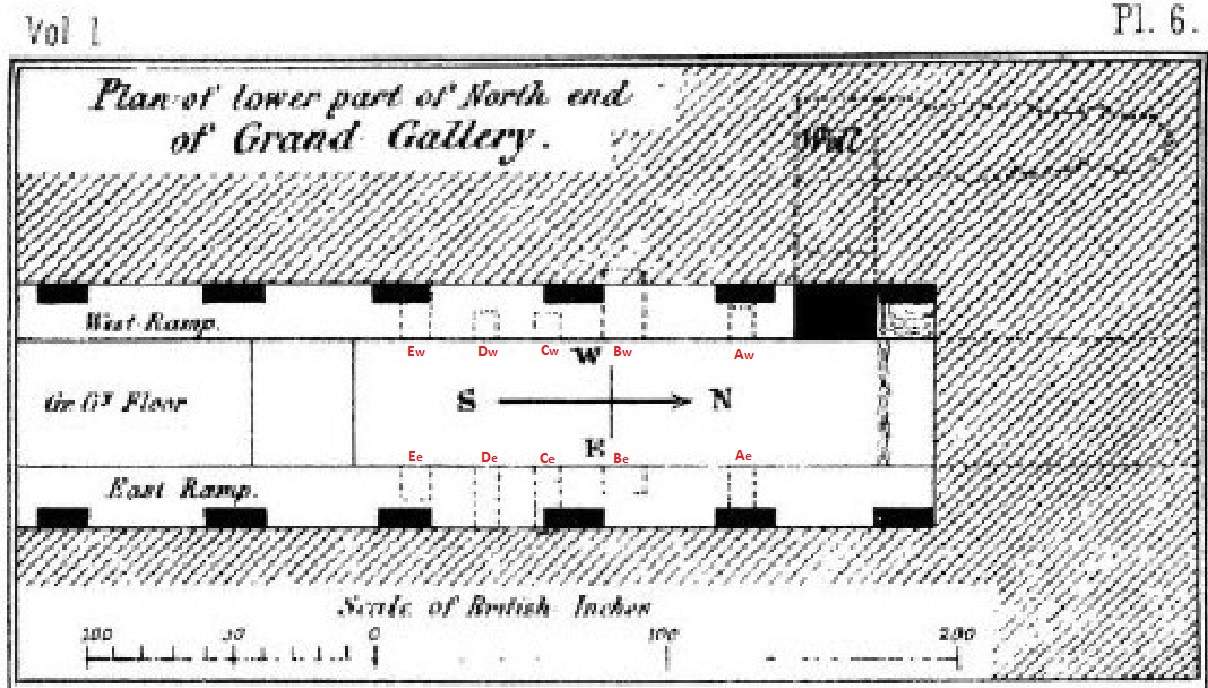
Underneath is the mentioned drawing:Source: S.22. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, 3 volumes, Edinburgh, Edmonston And Douglas 1867. Plate 6, P166 in volume 1.
Source: S.22. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, 3 volumes, Edinburgh, Edmonston And Douglas 1867. Plate 6, P166 in volume 1. (Revised version)
Position number 1, 2, 23, 24, 25 and 26 are known reference points.
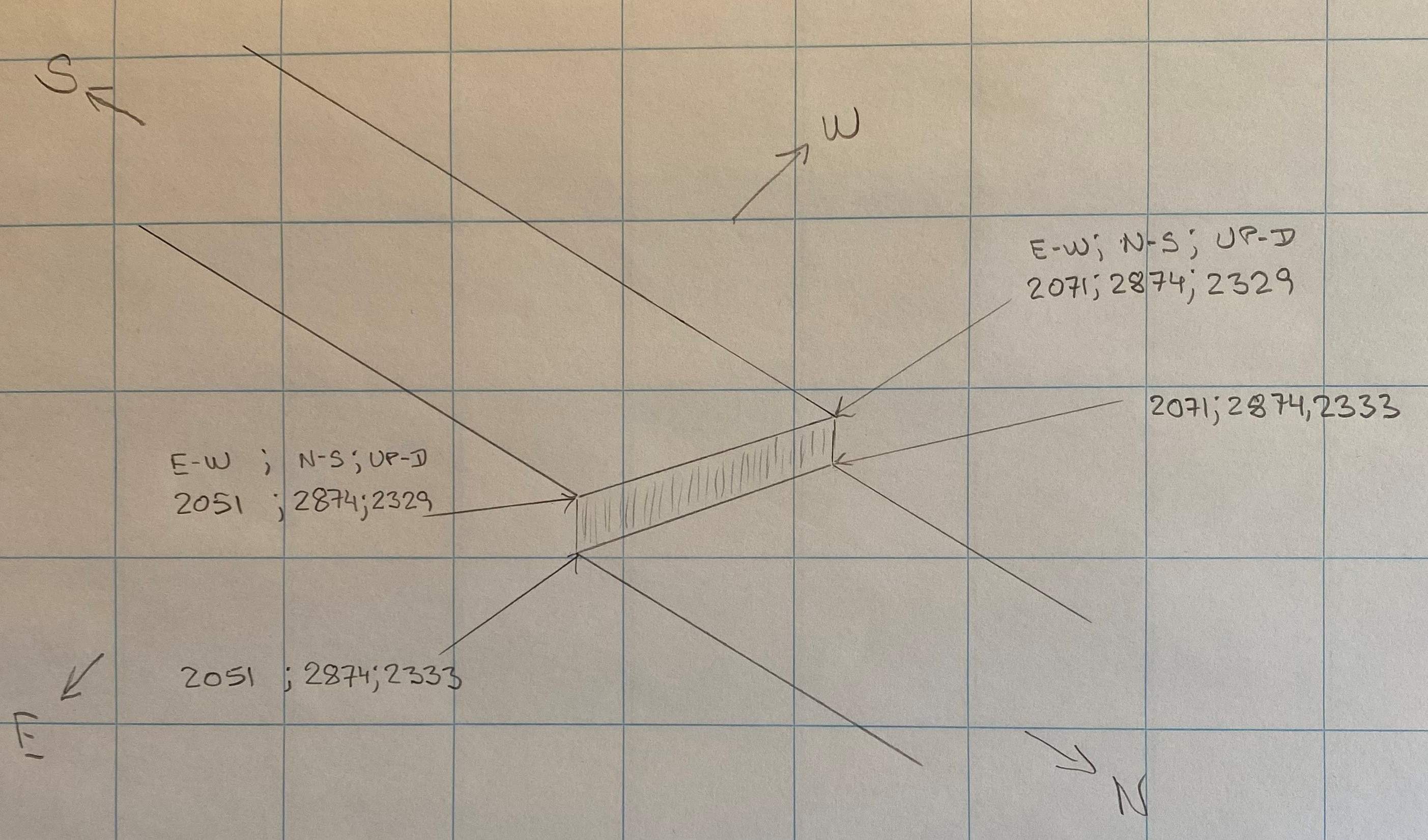
From section 5.5.10 and 5.5.20 we know the E-W coordinates of the positions (on the western side) 3, 6, 7, 10, 11, 14, 15, 18, 19, and 22 : 2071From section 5.5.10 and 5.5.20 we know the E-W coordinates of the positions (on the eastern side) 27, 30, 31, 34, 35, 38, 39, 42, 43 and 46 : 2051
First of all we need to convert the scale in British Inches to cubits.
The scale is from -100 inches to +200 inches which gives a span of 300 inches. In the Microsoft Paint the span is 171 pixels.
300 inches / 869 pixels = 0,3452
The factor between the British inch and the cubit is 1/20,62
0,3452 / 20,62 = 0,01674
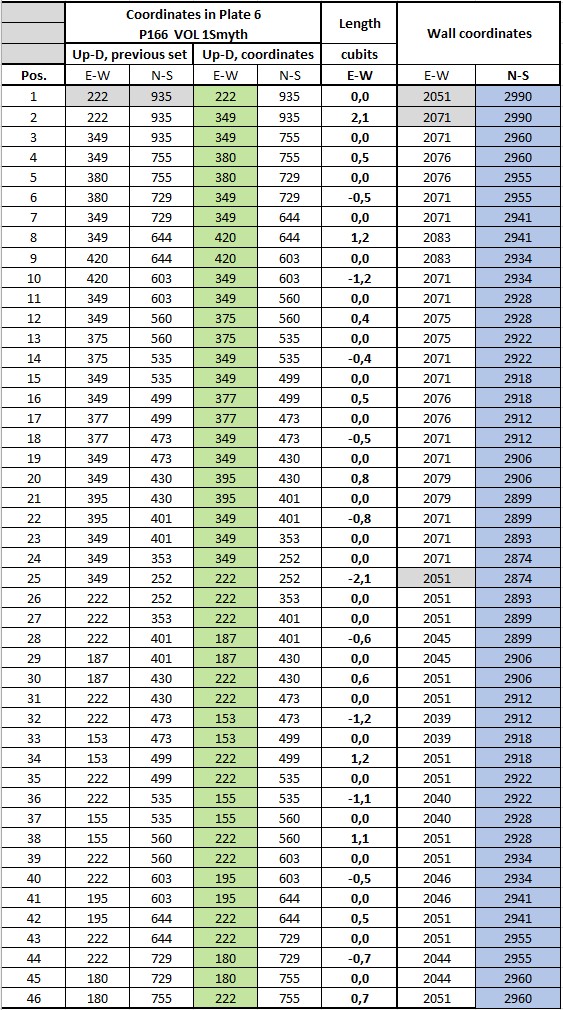
The horizontal dimensions and coordinates in E-W and N-S directions are:
The coordinates marked blue are readings from the table in section 5.7.3. The grey marked coordinates are reference points as described above and overrule the calculation method.
The readings of the N-S values are not used here as we already know the positions from section 5.7.3.
Calculation method:
Example based on pos. 4:
380 pixels(drw) - 349 pixels(drw) = 31 pixels(drw)
31 pixels(drw) x 0,01674 = 0,5 cubits
E-W coordinate 2071 (pos 3) + ( 0,5 cubits x 10 ) = 2076, which is the E-W coordinate in pos. 4
N-S coordinate is informed in section 5.7.3 and transferred to the table.
The coordinate for pos. 4 is then 2076;2960
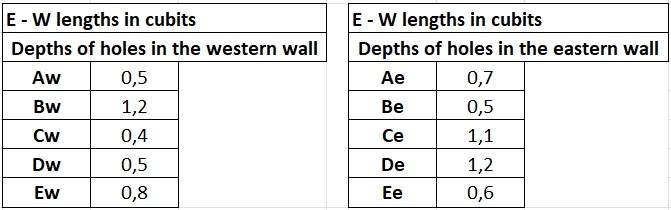
Here is in an overview of the depths of the holes:
Source: S.22. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, 3 volumes, Edinburgh, Edmonston And Douglas 1867. Plate 6, P166 in volume 1. (Revised version).
The depths are extracted from the above table.
It is surprising to see the depths of the mirrored holes in the eastern and western walls are not the same.
Section 5.7.5
The wooden bridge theory:
The functionality of the holes is unknown.
However, the holes opposite to each other have the same N-S Up-Down dimensions, which indicates they are connected to each other. If the depth of one hole in one of the walls is short, then the opposite hole in the other wall is long. The reason could be a wooden beam was inserted in the long hole, then the other end of the wooden beam could have been inserted in the opposite short hole to make a wooden bridge across the passageway from the eastern ramp-bench to the western ramp-bench.
It is also possible wooden planks have been mounted on the wooden beams to connect the floor of ramp starting from positions 24 and 24, ending at the end of the ascending passageway at the point 1 and 2.
I have tried to add the wooden beams in the drawing of Smyth, just to give an impression of how the holes were used. Unfortunately, I have no evidence, it is only a plausible theory. Of course I have no dimensions of the wooden beams, but theoretically they should fit inside the holes and not be too long because of the mounting.
In the drawing I have chosen a length of the wooden beams of 2,5 cubits. As there are 2 cubits RM from wall to wall, then the wooden beams are inserted by :(2,5 cubits - 2 cubits RM)/2 = 0,25 cubits or 7 fingers in each hole, which ought to be sufficient.
Source: S.22. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, 3 volumes, Edinburgh, Edmonston And Douglas 1867. Plate 6, P166 in volume 1. (Revised version - top view).
I have tried to add wooden planks in Edgar´s drawing:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 (page 64) (Revised version)
If we zoom in:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 (page 64) (Revised version)
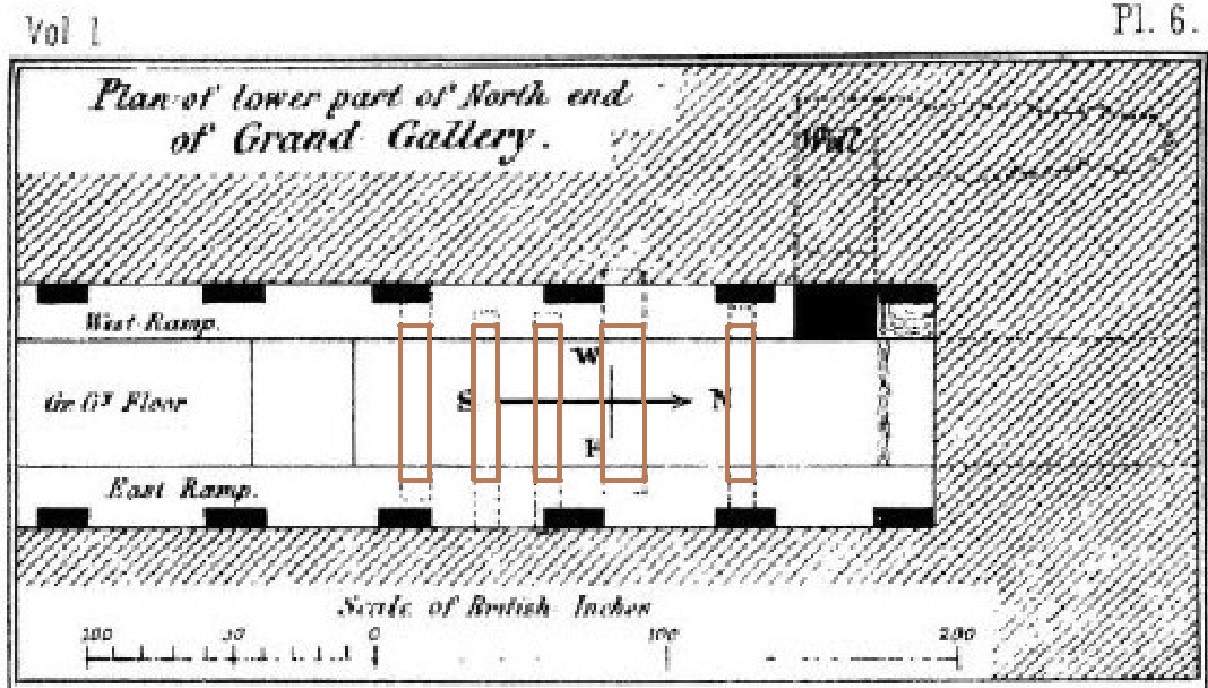
The wooden plank structure into the drawing of Piazzi Smyth:
Source: S21, The Great Pyramid Its Secrets and Mysteries Revealed, Plate XIII between pages 226 and 227 after the chapter "Corrigenda". (Revised version).
We zoom in a bit:
Source: S21, The Great Pyramid Its Secrets and Mysteries Revealed, Plate XIII between pages 226 and 227 after the chapter "Corrigenda". (Revised version).
We may assume the upper part of the planks follow the floor line of the ramp. The lower part of the planks hit the holes. in the table underneath in section 5.7.6 you can read exactly where they hit.
Section 5.7.6
In section 5.6.5 I showed this drawing:
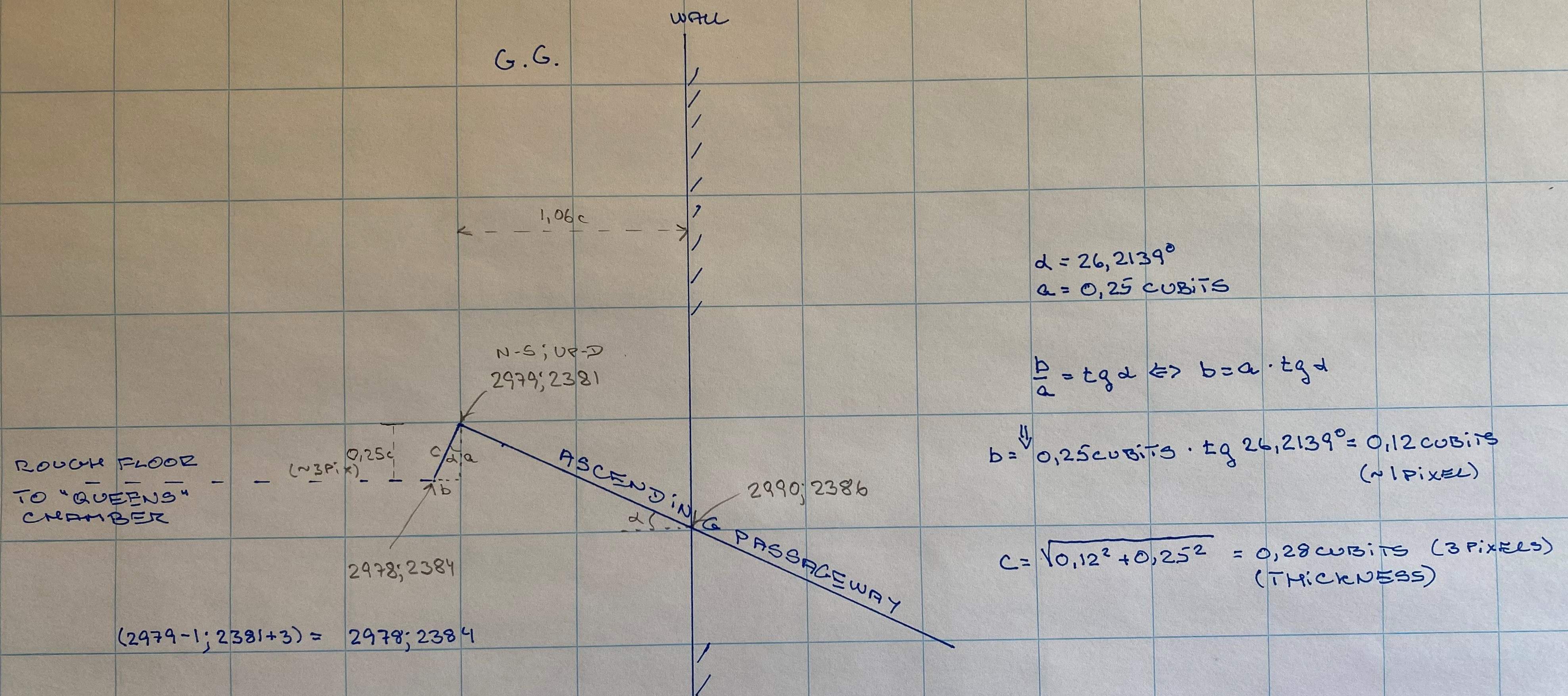
Pos. 2 has the coordinate 2979;2381 ( = POS. 14 in the revised drawing )
Pos. 5 has the coordinate (2979 - 1 ; 2384) = 2978;2384 ( = POS. 13 in the revised drawing )
Calculation method for pos 5:
0,25 cubits x tan 26,2139° = 0,12 cubits (= 1 pixel) in the N-S direction. 2384 is the up-down coordinate.
These two positions are reference positions in the table underneath.
Calculation method:
The scale is the same as used in section 5.7.2
The upper length of the planks from position 1 to 14 is:
The lower length of the planks from position 2 to 13 is:
From pos. 1 and pos. 2 in the above table we can calculate following:
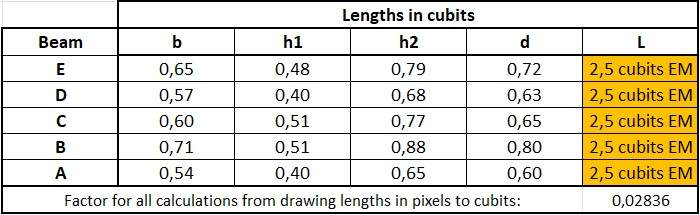
The vertical height of the planks are: (319 - 306) x 0,02836 = 0,37 cubits ( in the table above it is rounded up to 0,4 cubits ) ( = 19,4 cms).
The thickness of the planks are: (319 - 306) x 0,02836 x SIN (90° - 26,2139°) = 0,33 cubits ( = 17,3 cms)
The same table, but with two digits in the "Lengths in cubits" marked yellow:
Section 5.7.7
It seems there at least two different forms of cross sections of the beams: Either they are rectangular or trapezoid.
In the drawing underneath you can see a rectangular beam supporting the wooden plank by a corner. If the three plug blocks in the lower part of the ascending passageway were resting on the planks, it is hard to believe the planks and the corners of the beams could carry the heavy granite stones.
The weight of each stone is:
(1,9 cubits x 0,5236 meters/cubit x 2,29 cubits x 0,5236 meters/cubit x 3,33 cubits x 0,5236 meters/cubit ) x the approximately density 2.750 kgs/m3 = 5.719,59 kgs each.
It is 17.158,77 kgs in total.
Another solution could have been trapezoid formed beams, which could support the wooden planks and the granite stones much better:
Section 5.7.8
I have tried my best to draw a trapezoid beam.
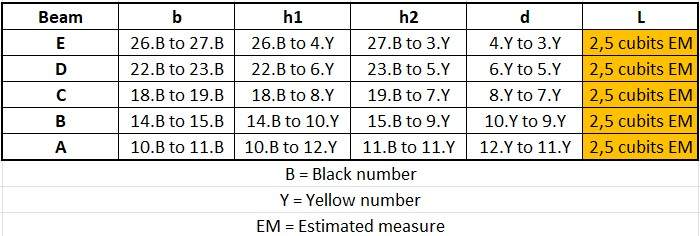
From the sections 5.7.2, 5.7.3, 5.7.5 and 5.7.6 we can calculate the beams had following measures (if they really existed):
Section 5.7.9
The yellow numbers refers to the table in section 5.7.6
The black numbers refers to the table in section 5.7.3
The drawing is combined by the drawings in section 5.7.2 and 5.7.5
Overview of the different lengths referring to the drawing in section 5.7.8:
Section 5.7.10
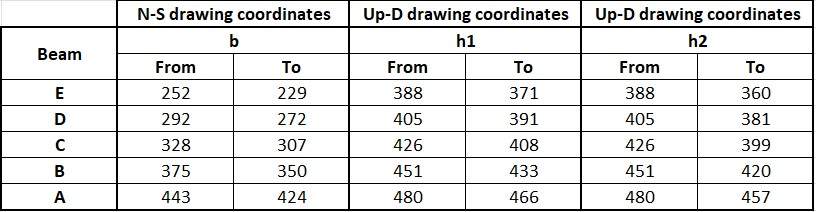
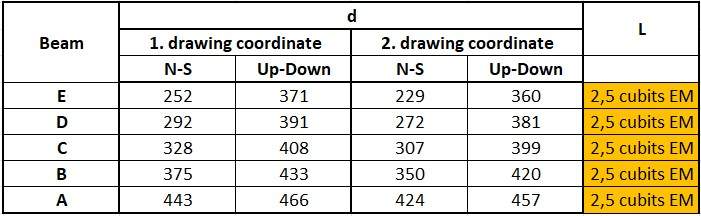
Drawing coordinates in pixels (first part):
Drawing coordinates in pixels (second part):
Calculated lengths:
Calculation methods:
Lengths "b", "h1" and "h2": Subtraction of the value in the field "From" from the value in the field "To" for each beam.
The lengths in "d" followed:
Section 5.7.11
An interesting observation: The blind passageway to the South of the subterranean chamber can contain all these beams and the wooden bridge as the dimensions of the passageway is much bigger, please see section 5.3.17 and 5.3.13, the drawings are shown underneath:
In section 2.3.3 (Mould - and soil?), I have referred to Edgars observation about the "mould" on the floor in this passageway:
In the book "Great Pyramid Passages" volume I by Edgar in 1910 :
My comments:
It is not likely the mould can grow on a floor of rock in a layer of 3 inches = 7,6 cm. There might have been a layer of organic material like wood or soil on which the mould could grow.
It could be the remains of the beams and wooden planks from the construction. The theory is, when the workers closed the pyramid by sending the 3 plug blocks downwards in the ascending passageway, they escaped through the shaft in the north-west corner of the Grand Gallery bringing all the wooden accessories with them and saved the planks and beams in the blind passageway.
But, is there enough space in the blind passageway for the 5 thick, short beams and the long planks ?Section 5.7.12
We know there are 5 beams estimated 2,5 cubits long, but we have no clue about the number of planks.According to section 5.5.10 the width between the ramp-benches is 2,0 cubits RM, which is 2,29 meters. It is not realistic they used only 1 plank of 2.0 cubits.
If we search for "normal" planks in stores nowadays, most of them has a width between 100mm and 200mm, which is between 0,19 cubits and 0,38 cubits, as they are easy to handle.
The width of 2 planks was 2,0 cubits / 2 = 1,0 cubits (= 524 mm).
The width of 4 planks was 2,0 cubits / 4 = 0,5 cubits (= 262 mm).
The width of 5 planks was 2,0 cubits / 5 = 0,4 cubits (= 209 mm)
The width of 6 planks was 2,0 cubits / 6 = 0,33 cubits (= 173 mm), which is in the upper end of the "normal" range.
The width of 7 planks was 2,0 cubits / 7 = 0,29 cubits (= 152 mm), which is within the "normal" range.
The width of 8 planks was 2,0 cubits / 8 = 0,25 cubits (= 131 mm), which is within the "normal" range.
The width of 9 planks was 2,0 cubits / 9 = 0,22 cubits (= 115 mm), which is within the "normal" range.
The width of 10 planks was 2,0 cubits / 10 = 0,2 cubits (= 105 mm), which is in the lower end of the "normal" range.
Before we choose a possible width we need to check the thickness, maybe there is clue here:
According to section 5.7.6 the vertical height is 0,25 cubits and the horizontal displacement is 0,12 cubits, which gives a thickness of 0,28 cubits.
Calculation method:
Considering they did not work with planks, but only with beams, then they could have used 7 beams of 0,28 cubits x 0,28 cubits x the length ?
(7 x 0,28 cubits = 1,96 cubits which gives a bit space if the beams were not 100 % straight.)
Section 5.7.13
Here is a drawing - a top view - where you can see where the extended floor of the ascending passageway end in the Grand Gallery and the lower position of the 7 beams, (if they existed):Section 5.7.14
Underneath is a drawing and calculation of where the extension of the floor of the ascending passageway hits the floor to the "Queens chamber".The thickness of the possible beams must have been 0,28 cubits.
Section 5.7.15
Underneath is a drawing of the upper part, where the possible beams joined the ramp floor:Section 5.7.16
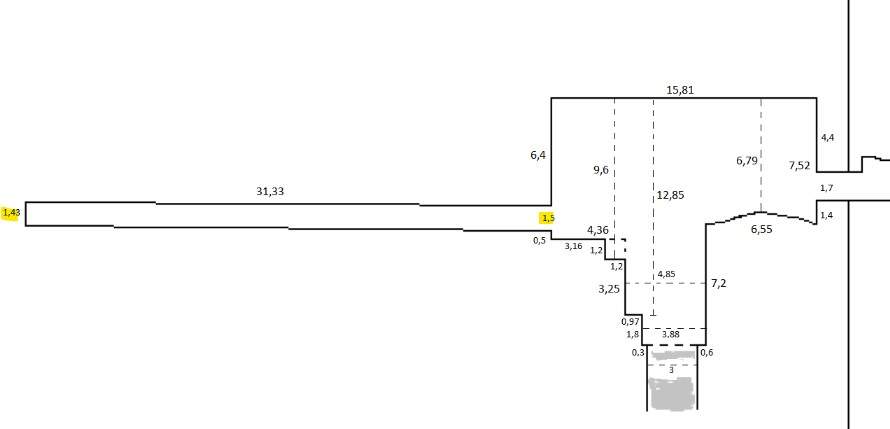
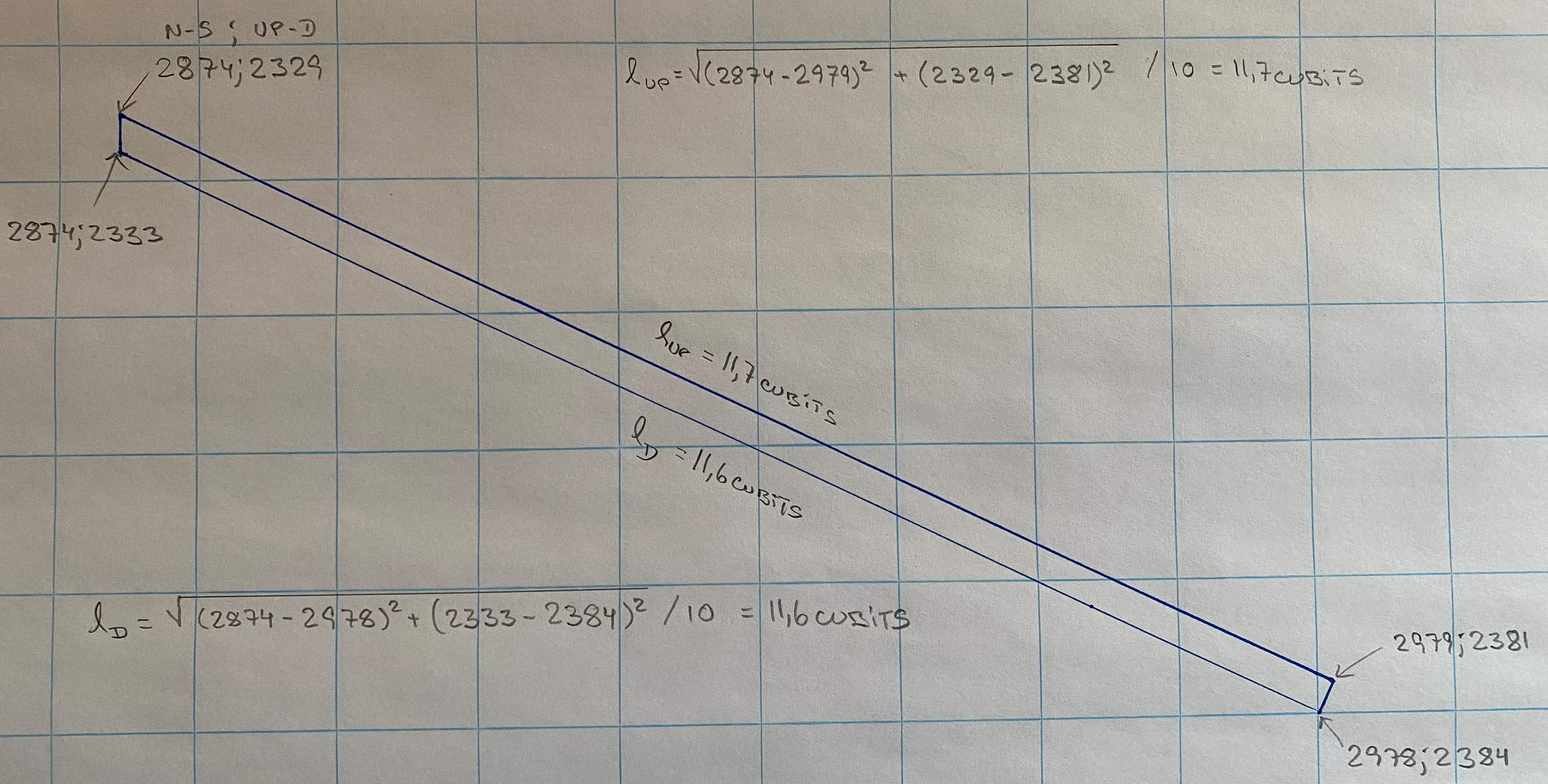
Underneath is a drawing of a possible beam and a calculation of the length:11,7 cubits (= 6,1 meters) is a bit long - but possible.
The question is whether they could be transported in their original length downwards through the Shaft ? Maybe the saw them into smaller pieces - for example 6 cubits.I have read a question during my work on this web site, why the Shaft was not more vertical and hit the descending passageway higher.
I think the answer is, the long beams could not be moved into the descending passageway if the Shaft was too vertical. Instead the shaft was bended towards south to hit the descending passageway far lower, so it was possible to move the long beams directly into the blind southern passageway.
Section 5.7.17
One of my readers asked whether or not there was space enough in the southern horizontal passageway for all these wooden beams. To answer this properly I have some models of the wooden beams:On the left screen behind you can see the drawing of the holes (A to E) and in the front you can see models of the beams, respectively.
The dimension ratio of the models is 1 cubit corresponds to 1 cm.
The next picture shows the 5 models of the wooden beams, the models are made of cardboard and apologize the lack of artistic execution. The most important issue is, that all dimensions are correct:
The most southern part of the horizontal passageway, after the bend, is shown here. The dimension ratio is of course the same :
How does it look like if I try to place them in the passageway model?
They seems to be too big, but if I combine them, then something magical happens:
If I combine beam A and E together and beam C and D together, then they fit perfectly.
What about beam B? There is space enough in bending passageway:
So the solution for all 5 beams is:
Please ignore the bended part of the passageway is moved away due to lack of space on my table.
The height of the most southern part of the blind passageway is 1,43 cubits and the highest combination of the beams is 0,84 cubits.
Section 5.7.18
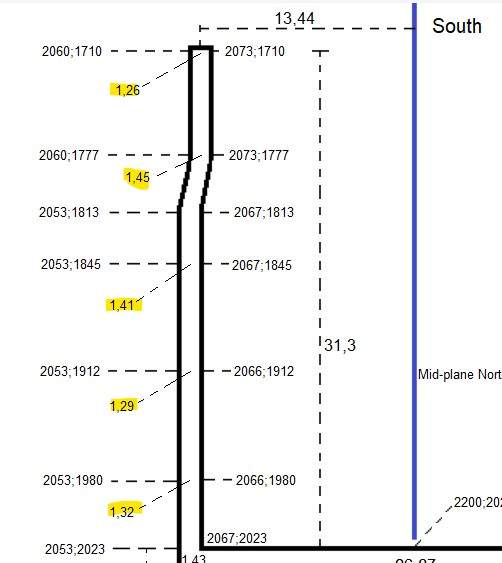
The 7 long wooden beams, which were a part of the "bridge", were stowed away in the northern part of the horizontal passageway close to the entrance to the subterranean chamber.
If they were collected together they fitted into the passageway without any problems. I have made a model to show how they could have been stowed away. Please also be aware, that each of the wooden beams were 0,28 cubits wide and the height was 0,28 cubits as well. so the total dimension in those two directions were max. 3 x 0,28 cubits = 0,84 cubits and the width of the northern part of the passageway is 1,29 cubits to 1,41 cubits; the height is 1,5 cubits .
On the right screen behind, you can see how the 7 beams formed a "bridge".
The northern section of the passageway before the bend is (2023-1813)/10 = 21 cubits long and the long beams were 11,6 to 11,7 cubits long - so plenty of space for these as well.
The conclusion is the theory about the wooden beams and how they were stowed away, seems to be possible.
Why did they keep the beams in the building?
One more question: Why did they bury a ship outside the masonry?
I think the answer is the same. King Khufu needed the wooden bridge and the
ship when his souls travelled. I mean, not necessarily at the same time, but I
think it was important both items were available. You can see similar offerings
in other graves, where the body was buried together with for example weapons,
food or other items which were important for the soul of the dead.
Was the wood at all used, what kind of wood was it and maybe it was reused?
In the Journal of Egyptian History 6 (2013) 152–176, Pearce Paul Creasman wrote the article "Ship Timber and the Reuse of Wood in Ancient Egypt*" about the subject.From the Abstract it is clear reuse of materials hereunder wood was common in the ancient Egypt.
In the Introduction it is mentioned that a huge amount of wood was imported from the Near East, Byblos?, during the Old Kingdom. The Khufu I vessel was build of more than 38 tons of imported cedar, source: Mark, “Construction,” 133.
More important is the chapters "Reuse of Ship Timbers for Burial Linings, Coffins, and Other Wooden Objects", "Reuse of Ship Timber in Earth Construction and Temporary Structures" and "Conclusion", pages 163 - 172 which indicates, it was very likely phragments of old boats of timber was used elsewhere for example in constructions.
The theory of the wooden bridge in the Grand Gallery seems to be well supported by this article.
Section 5.7.19
As a little curiosity I can mention the form of the 5 wooden beams were not completely unknown, please see the next picture. Please compare the beam with the form of the casing stones, source: https://commons.wikimedia.org/wiki/File:Cheops_pyramid_02.jpg :
Another point of interest is these two pictures, please see the vertical lines on the stone above the entrance of the horizontal passageway:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910
I have added some yellow help lines:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 with my yellow help lines.
It is not clear whether these lines are made during the construction of the Grand Gallery or they are applied later on.
However, they might be a kind of marks from wooden beams which could have supported the wooden bridge or the other wooden beams. If they supported the wooden bridge they must have been standing on the floor, which prevented, at least for a period of time, the access to the horizontal passageway and the Queens chamber and hindered the floors to be finished.
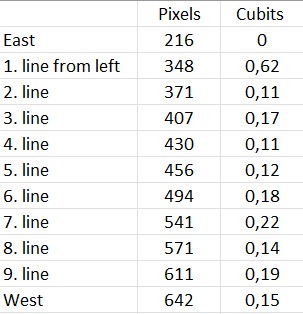
I have measured the pixels from left to right, meaning from east to west and calculated the cubits between the yellow lines:The calculation method:
The width of the stone is 2 cubits RM.
The eastern corner has the pixel: 216
The western corner has the pixel: 642
The distance from eastern corner to the first detected line is: (348 pixels - 216 pixels)/(642 pixels - 216 pixels) x 2 cubits = 0,62 cubits
The distance from the first detected line to the second line is: (371 pixels - 348 pixels)/(642 pixels - 216 pixels) x 2 cubits = 0,11 cubits
and so on ...
We return to section 5.7.2 and continue to investigate the horizontal passageway.
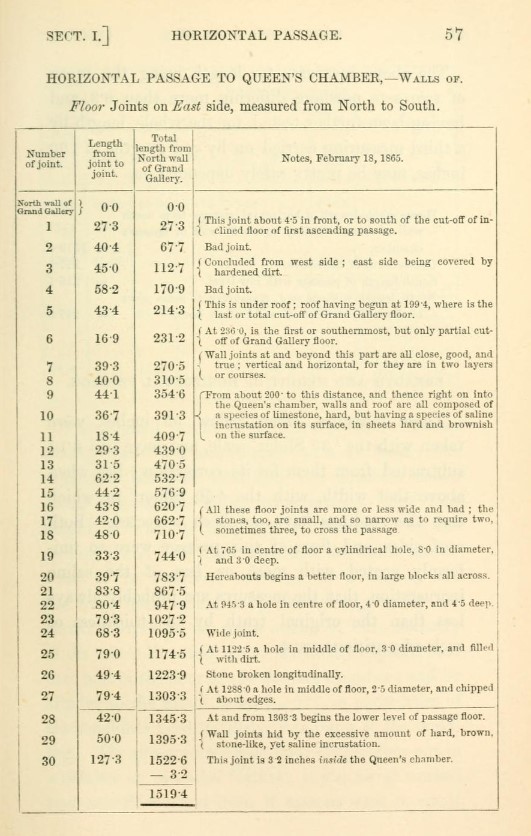
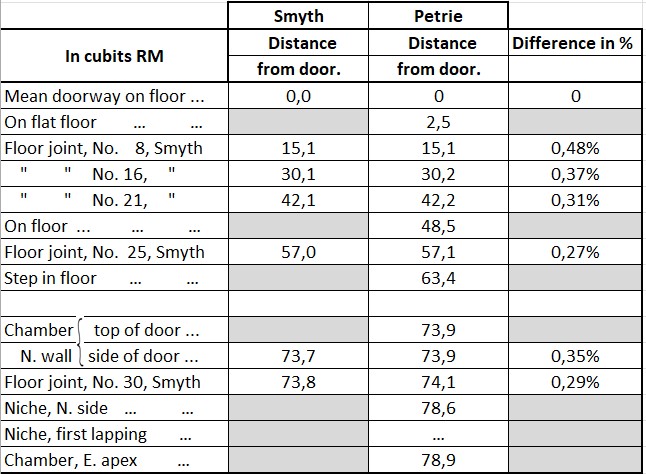
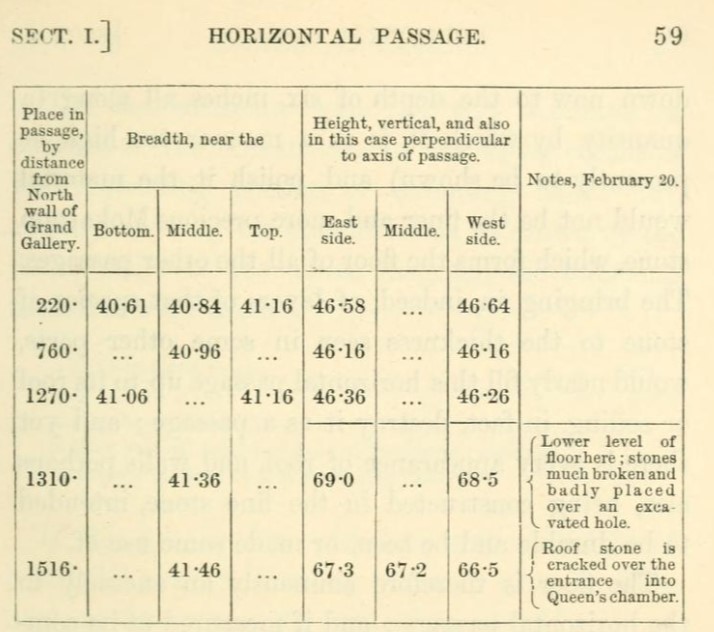
Petrie made these measurements:
Source: (S5 orig-[S40]-P66-L5), table.
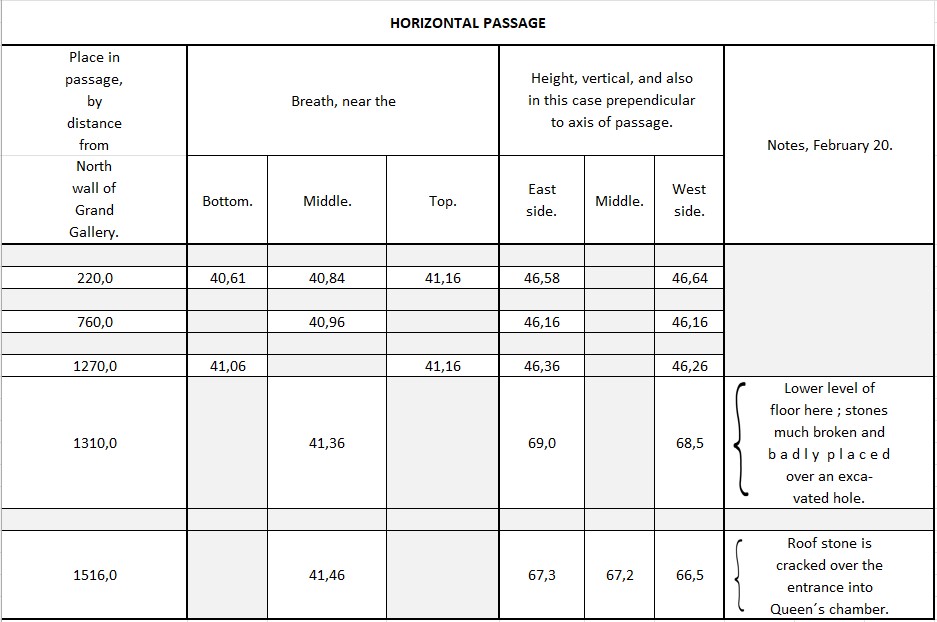
To process above data easier, I have transferred the measures to an Excel sheet:
The measures are in inches.
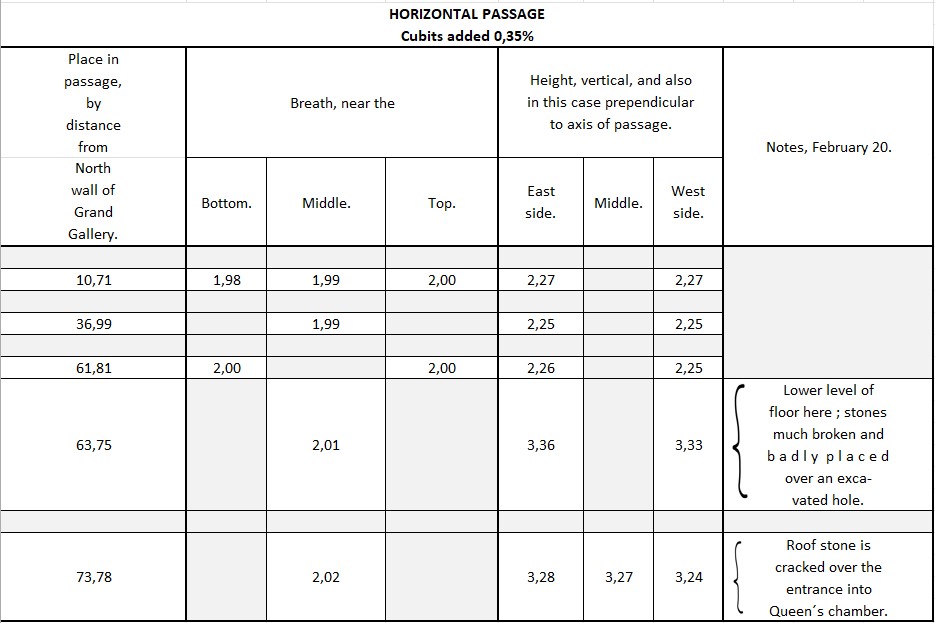
The same table in cubits RM:
Section 5.7.21
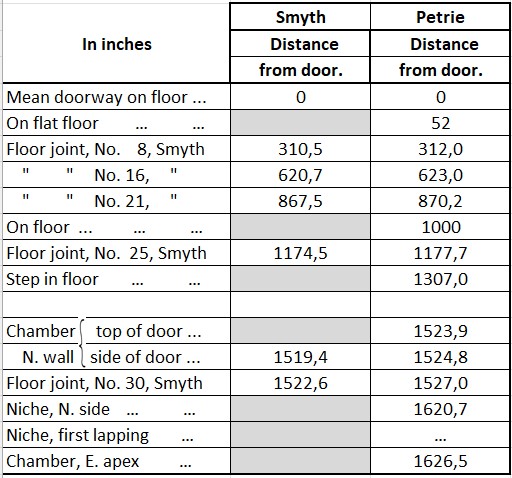
Let us compare these measures with the measures made by Smyth.Here are the measures of the horizontal passageway by Smyth:
S.20. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, Vol. II, page 57.
Hereunder I have compared the measures and it seems Smyth had a problem with the measurements. I think Petrie suspected this from the very beginning and this one of the reasons Petrie made this work with new measurements.
It is clear Smyth measured the lengths shorter and the deviations ranges from 0,27% to 0,48% with an average deviation of 0,35%.
Smyth mentioned in his book "The Great Pyramid Its Secrets And Mysteries Revealed" source S21, page 96:"1 Pyramid cubit = 25,025 British inches = 25,000 Pyramid inches"
The difference of those two types of inches is (25,025-25,000)/25,025*100 = 0,1% so this cannot explain the above calculated differences.
I am not sure whether or not the differences are existing for the horizontal passageway only or maybe it is general bias caused by his measuring instruments.
For this passageway we take Petrie's measures for granted and if we must use Smyth's measures then we are forced to correct them by 0,35% or multiply by a factor 1,0035.
The units of Smyth´s measures will be in cubits - not in cubits RM, because the results are calculated.
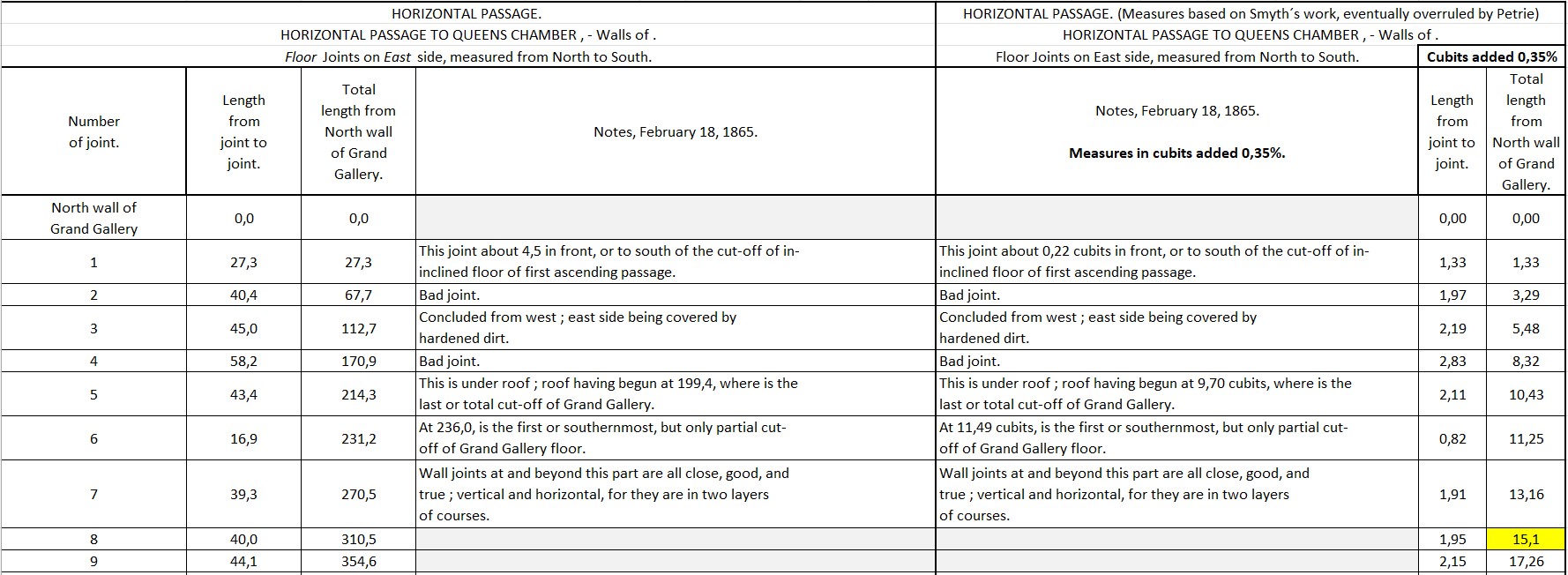
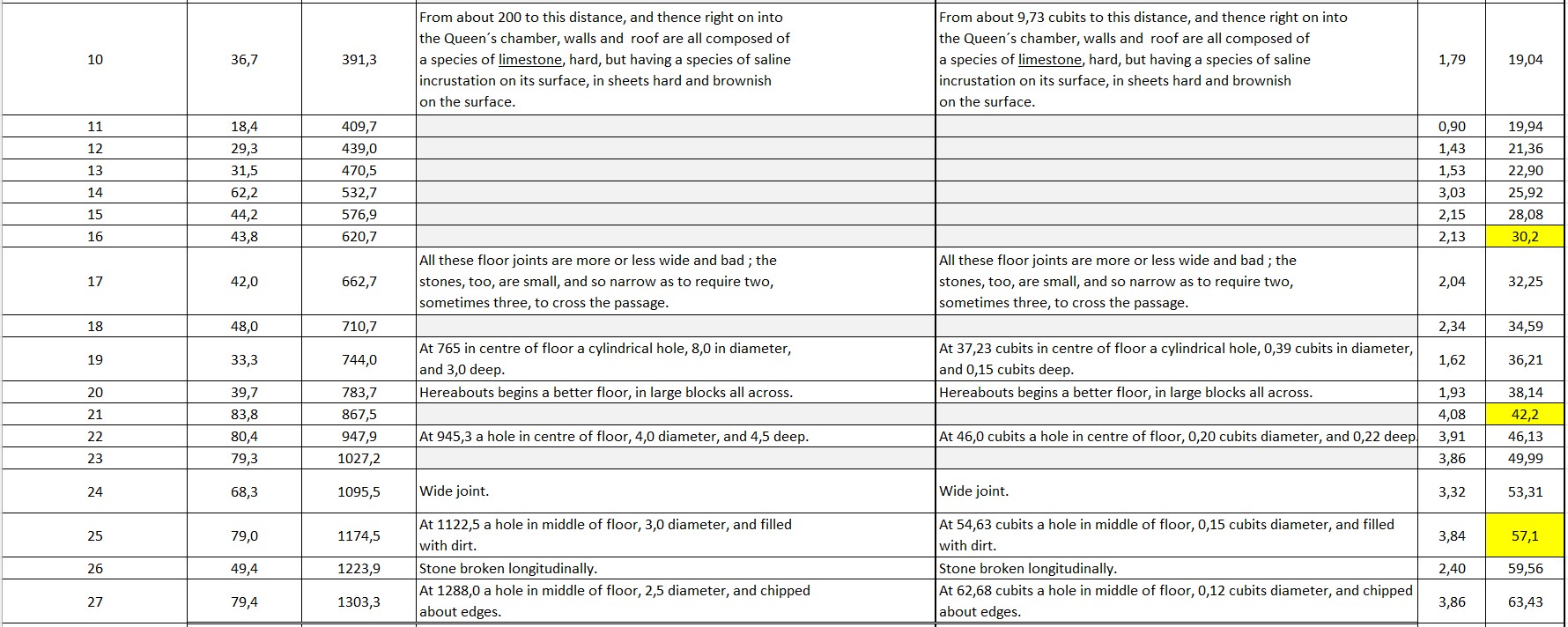
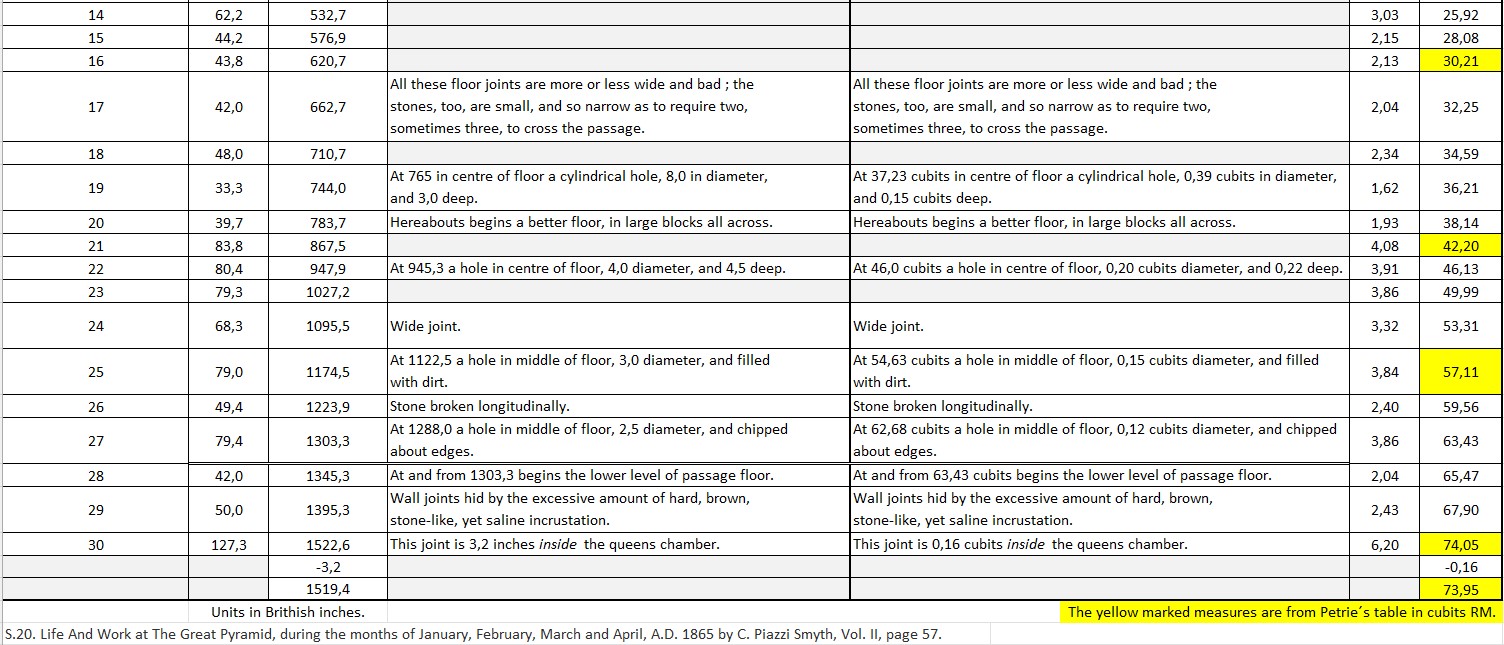
Section 5.7.22
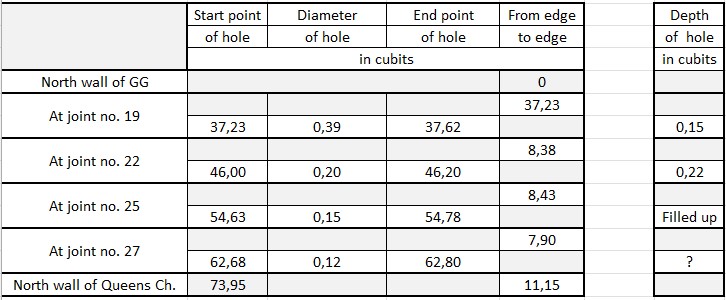
Based on the table in section 5.7.21 and with the replacements by the Petrie´s measures I have converted the units into cubits:Smyth observed and mentioned 4 holes in the middle of the passageway at the joint numbers 19, 22, 25 and 27; respectively at 32,27 cubits; 46,0 cubits; 54,63 cubits and 62,68 cubits from the northern wall in the Grand Gallery.
Here is an overview of the holes in the floor of the passageway:The sum of the "Diameter of hole" and the sum of the "From edge to edge" makes 73,95 cubits.
It seems there is a pattern concerning these holes. Please see the drawing in section 5.7.24.The roof of the passageway begin at 9,70 cubits and the partial cut-off of the Grand Gallery floor is at 11,49 cubits.
From the start point to the northern wall of the "Queens chamber" there is a length of 73,95 cubits - 62,68 cubits = 11,27 cubits.
The distances from edge to edge of the holes are approximately the same ranging from 7,9 cubits to 8,38 cubits; a difference of 0,48 cubits or 0,25 metres.
The purpose of these holes is unknown.
Section 5.7.23
Smyth measured the width and height of the horizontal passageway:S.20. Life And Work at The Great Pyramid, during the months of January, February, March and April, A.D. 1865 by C. Piazzi Smyth, Vol. II, page 59.
The units in the table are British inches.
I have transferred this table into an Excel sheet:
When converting these measures to cubits we need to add 0,35%.
Underneath is the same table but the measures are in cubits:Calculation method : Inches x 1,0035/20,62 , the units are cubits.
In my drawings the width will be with 1 digit, so the result will be 2,0 cubits (=20 pixels), which is also the average of the measurements.The height changes all of a sudden after 63,43 cubits from the northern wall of the Grand Gallery. It is 2,27 cubits at the doorway but is lower inside the passageway; around 2,25 cubits. At and from 63,43 cubits it seems the floor is not finished and the height is much more irregular ranging from 3,24 cubits to 3,36 cubits. In the doorway to the Queen´s chamber the height is 3,27 cubits (=33 pixels).
Section 5.7.24
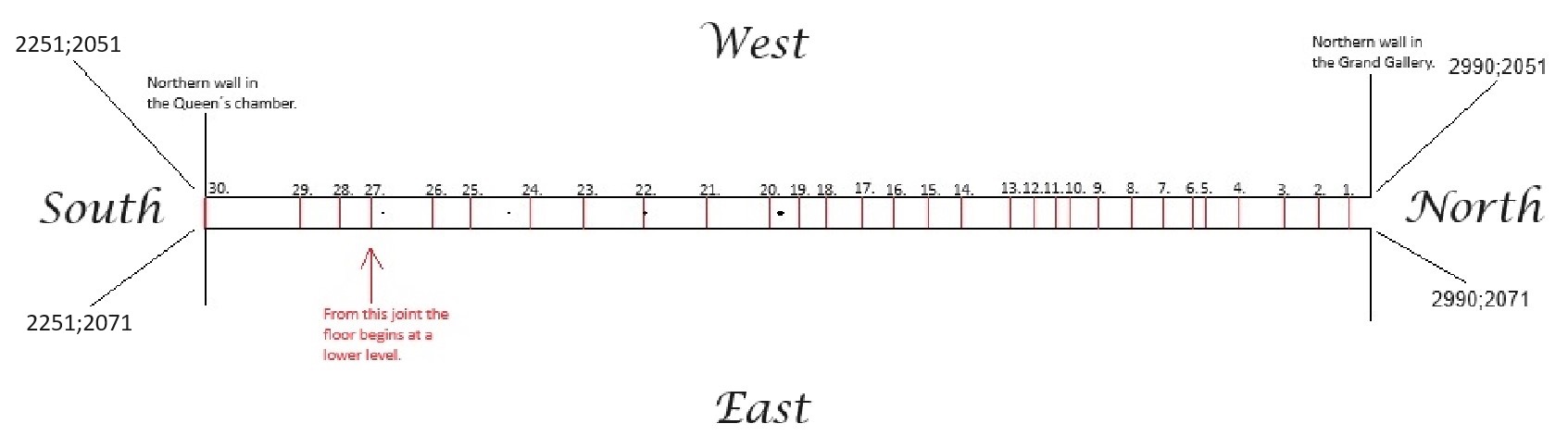
Underneath is a drawing of the the horizontal passageway starting from from the northern wall in the Grand gallery to the northern wall in the Queen´s chamber:Top view of the passageway. The numbers refer to the joint numbers in the table in section 5.7.22.
From the joint 20 and to the northern wall in the Queen´s chamber the stones are larger.
From the joint number 27, the floor is lower.
The complete floor, from the beginning to the end, appears rough and not polished, which is unusual in this pyramid.
I have added the 4 holes in the centerline of the passageway mentioned in other the table in section 5.7.22.
The first hole of these 4 holes between joint number 19 and 20 begins at 37,23 cubits and ends at 37,62.
The complete length of the passageway is 73,9 cubits. Half the way is 73,9 cubits / 2 = 36,95 which is quite close to the first hole.
The roof starts at 9,70 cubits between joint numbers 4 and 5.
The lower level of the floor begins at 63,43 cubits RM just after the 4th hole.
The length from the northern wall of the Queen´s chamber is 73,9 cubits - 63,43 cubits = 10,56 cubits.
Could the holes have played a role in the transportation? if so; then the 2nd hole in the joint 27 does not make sense.
Maybe the holes are made by a coincidence - or - perhaps they are markings for a specific purpose. If there is something I really wish in my life, then it is to find the manual for this magnificent and mysterious building.
The shown coordinates are N-S;E-W.
The length of the passageway is 73,9 cubits. The northern N-S coordinate part is 2990 acc. to section 5.7.4, the southern is 2990-739 pixels = 2251.
Section 5.7.25
The horizontal passageway has these measures and coordinates:
According to section 5.7.20 Petrie measured the levels of the roof and the floor of the passageway and both descend from north to south until the step near the Queen´s chamber.
1a. At the floor joint, no. 8, Smyth, the floor level at the distance 15,13 cubits RM from the door (or northern wall) is 41,58 cubits RM equal to 416 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 416 =2384.
1b. At the floor joint, no. 8, Smyth, the roof level at the distance 15,13 cubits RM from the door (or northern wall) is 43,83 cubits RM equal to 438 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 438 =2362, which is 0,1 cubits (or 1 pixel) less the roof level where the roof begins. The height of the passageway at the floor joint no. 8 is decreased to (2384 - 2362) / 10 = 2,2 cubits.
2a. At the step in the floor, at the distance 63,39 cubits RM from the door (or northern wall), the floor level is 41,40 cubits RM equal to 414 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 414 =2386.
2b.
At the step in the floor, at the distance 63,39 cubits RM from the door (or northern wall), the roof level is 43,70 cubits RM equal to 437 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 437 =2363, which is 0,2 cubits (or 2 pixels) less the roof level where the roof begins. The height of the passageway at the step in the floor, just before the step
is increased to (2386 - 2363) / 10 = 2,3 cubits.
3a. At the step in the floor, at the distance 63,43 cubits from the door (or northern wall), the floor level decrease to 40,50 cubits RM equal to 405 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 405 =2395.
3b. At the step in the floor, at the distance 63,39 cubits RM from the door (or northern wall), the roof level is 43,70 cubits RM equal to 437 pixels. the total height of the pyramid is 280 cubits NM equal to 2800 pixels. The coordinate for the level of the floor at that point is 2800 - 437 =2363, which is 0,2 cubits (or 2 pixels) less the roof level where the roof begins. The height of the passageway at the step in the floor, just before the step is increased to (2365 - 2363) / 10 = 3,2 cubits, which seems to be unchanged to door opening at the Queen´s chamber.
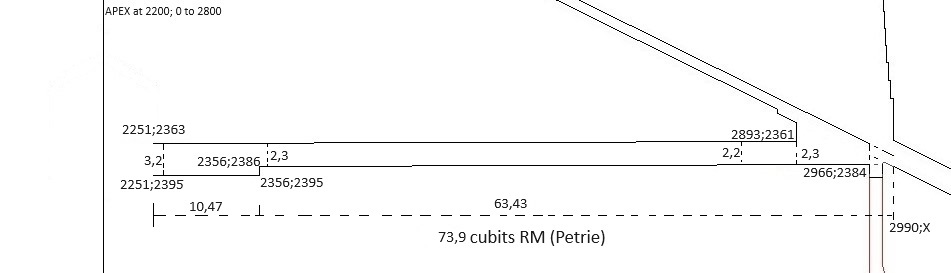
The two coordinates at the step in the floor:
(2990-634;2386) = 2356;2386
(2356;2386+9) = 2356;2395
The coordinates of the end of the passageway at the entrance to the Queen´s chamber:
Roof: (2990-739; 2363) = 2251;2363
Floor: (2990-739; 2395) = 2251;2395
Section 5.7.26
Here is two photos of the peculiar step where you can see the lower level of the floor in the horizontal passageway taken by Edgar:
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 , (page 294)
Source: The Great Pyramid Passages And Chambers" Volume 1 by John and Morton Edgar, 1910 , (page 295)
Section 5.7.27
Here is a top view of the horizontal passageway, the passageway is drawn in yellow:Here is a closer view of the beginning of the passageway:
The blue line indicates where the roof of the horizontal line begins.
Hereunder is a closer view of the most southern part of the horizontal passageway:
There are two interesting features here:
1. The floor step at the N-S coordinate 2356 in the horizontal passageway seems to very close in the north-south direction to where the descending passageway ends at floor level at N-S coordinate 2349 at the floor according to section 5.3.16. The difference is 7 pixels which is 0,7 cubits (= 37 cms) only. (The narrowed passageway begins at the N-S coordinate 2339, which leads to the subterranean chamber).
2. The horizontal passageway, which leads to Queen´s chamber, end at N-S coordinate 2251, which is very close to the beginning of the "Recess" in the horizontal passageway,
at N-S coordinate 2243 according to section 5.3.15 leading to the subterranean chamber. The difference is here 8 pixels which is 0,8 cubits (= 42 cms) only.